Finding Joy among the Skullduggery

How illegally crimped toilet paper and the French cheered me recently, amongst other things.

“Aurum ex stercore”¹

"Fear of Death does not prevent you dying: it prevents you living"

I am prompted to write this article by hearing several people say that they have had to have a break from concentrating on discerning the exact nature of the shitfuckery. (Apologies for the use of the vernacular, but in my household that word has become the standard way to refer to it after seeing videos by the Honest Government Ad. bunch. They produce some brilliantly funny, biting, educational satire; but they also promote CO₂ misinformation).

There’s only so much that an individual can take, and you have to have down time if you’re going to perform well in the long term.

(On the other hand I may be completely wrong. The people who are going flat out, like Mike Yeadon  or Jessica Rose amongst many many others, may well be more effective than I … what am I saying?! … of COURSE they achieve much more than me … Maybe they have a better appreciation of how desperate the situation is, and are quite rightly giving it their all, not taking breaks).

Anyway, on the off-chance that you would welcome a prompt to devote some time to appreciating life before you peg it, I’ve come up with four things (or types of thing) that recently have given me genuine joy, even in this melancholy present. There is a variety: the universal, the peculiar to me (but serves as an example); the  commonplace, and the unique.

I do trust this will not come across as “look how much I’m enjoying life”, but more in the spirit of Primo Levi’s “Moments of Reprieve”. (He wrote amazingly wise, human and insightful accounts of his life which centred around being a Jew in Auschwitz for a long time).

“Count your blessings” is not exactly an original thought; but I hope there is something new to you here that you will enjoy. I start with the commonplace and end with the unique.

1 Beautiful Nature
2 Loved ones
3 The French
4 2023’s “Everest”: Hats, Turtles and Spectres

---

1  Beautiful Nature

Too obvious to mention, and yet people often seem to appreciate being reminded.  Here are a few recent photos from the garden, which are pleasant enough.  I suspect that for actual joy, though, photos need to serve as reminders of the occasion when you actually had the experience of seeing such things in the real world.

Rosy-fingered Dawn

Dassie

A neighbour's horse enjoying our meadow

Sunbird in coral tree

Green beetle

Red beetle

Putting on a display

Butterfly (black)

Butterfly (tan)

Bee feast

Garden Produce

Mannekin conflab

Misty dawn

sunbird

The Moon

Here’s lookin’ at you.

---

2 Loved ones: Family and Friends

Most of us will be able to think of wonderful moments, whether from the present or past, that our family - (I include pets here!) - or other loved ones have given us, and it’s worth actually taking the trouble to recall those moments from time to time: to pick up the phone, or go through old photos, for example. My family members all invariably give me joy when I am with them; all too rare since we are spread over the globe, currently. My wife on the other hand ... gives me joy daily, of course! (By co-incidence she’s looking over my shoulder as I write)! ;-)

(No, really – she does)!

We all know that with family, joy is rarely unalloyed!  In my case some of my family are “vaccinated”, which gives me considerable anxiety. 

It's going to have to be your family, not mine, that give you actual joy.  E.g. I’m in the fortunate position of having about the cutest grand-daughter in the World, at about 9 months old. My son in Australia sends me weekly videos and stills of her and other aspects of life; and I’d love to include a picture, but there’s probably some reason why it wouldn’t be wise. Pictures of cute kids and animals are not hard to find!  But  it really needs to be your close relative for actual joy, as opposed to “mignonalgia” [meenyon-aljia] – a word we coined in our household for the reaction to cuteness which is so strong it hurts!

My parents are both dead, but the other day I came across a book that my wonderful sister put together, of my mother’s poems, and I was struck by how witty she was. I wish I had been more appreciative when she was alive - (as well as generally nicer to her). I'm going to share a very light-hearted one that she dashed off for “National Poetry Day” in the UK one year, which even people (like me) who generally don’t think of themselves as being “into” poetry should enjoy … (although my mother dismissed this one as “doggerel”). But of course to me it's evocative of my mother - not just a somewhat amusing poem.

National Poetry Day

No-one wants to work today:
It's National Poetry Day!  Hooray!

Tycoons forget their stocks and shares
And all the cares of current affairs;

Computer chaps switch of their screens
To conjure up idyllic scenes;

And buses stop as crews dispute
The merits of the trochaic foot.

Cabbies, flags down, smoke and frown,
Struggling to write their sonnets down;

And pretty debby girls in mews
Are writing witty terse Haikus.

Colonels in clubs write to the Times
Complaining modern poems don't rhyme.

While housewives, beds unmade, all hope
To write some verse like Wendy Cope.

Drivers of trains halt as they find
The wrong sort of words have blocked their lines.²

Captains far at sea heave to 
And give a day's leave to their crew

To write some sad and sweet sestinas
To newly deserted signorinas.

Farmers, milking, amuse their cowmen
By quoting the works of A.E. Housman.

Nurses ignore the cries of pain
To pen a new four line quatrain.

Schoolgirls sprawling in the dorm
Scrawl poems of love in rondeau form.

Typists in bedsits sit and sigh,
Thumbing the dictionary as they try

To versify as Dylan did.
Behind the bike-shed, safely hid,

Some horrid boys spray naughty verse,
All scatological - or worse.

Then as the shades of evening fall,
The day, they say, was fun for all;

And in the streets the people's feet are
Dancing to iambic meter.

---

3 The French

"The French" is a more provocative and striking title, but for more general appeal, perhaps the more honest title would have been “music and dance”.  

There’s a reason why much of the World uses the French expression “joie de vivre”. If you didn’t see this video of “Danser Encore” actually during the lockdown, then you must cast your mind back to what lockdown felt like. The whole point of the event this video records is that it was done around the nadir (the low point) of the Time of Lies. 

The French do many things well, and rebellion is one of them. When the EU first tried to stop French rustic markets from selling cheese in the way they had done for centuries, on hygiene grounds, it was largely met with a Gallic shrug, and ignored. I do hope that’s still the case.

This video always brings tears to my eyes. The event was a wonderful evocation of what it is to be genuinely human in this time of de-humanisation. You can see that at the start it’s a little stilted and “performed”, but they soon get into it, as the song and dance and esprit de corps work their magic, and you see the joy in the faces of passers-by, who watch or join in the dance, as they shrug off the grey collectivist dust.

[Edit: after a couple of days, according to the Substack statistics, out of the 170 people who read this article only 4 watched this video! IT’S THE MOST JOYOUS THING IN THE ARTICLE: do watch it!!]

Start with this one, my favourite, but if you don’t speak French, first familiarise yourself with the gist of the lyrics in English.  I think the words are remarkably perceptive and expressive, particularly when the lyricist is restricted (as ever in songs) by scansion and rhyme.

(This fairly literal translation destroys the rhyme and meter, as well as the puns.  Others have attempted to write equivalent sentiments in their own language, There are English, and again here; this one (Danzare Ancora) shows lots of places in Italy; Portugese and Spanish versions, e.g.). Here’s a whole “documentary”.

Danser Encore!     
To Dance Once more

[CHORUS]
Nous, on veut – continuer à dancer encore
We - we want to dance again!

Voir nos pensees enlacer nos corps
To see our thoughts embrace our bodies!

Passer nos vies sur une grille d’accords?
Spend our lives [restricted] [pun:] [in a grid of agreements?] / [on the [conventional] table of chords?]³

Oh non-non non-non non ...
Oh no-no, no-no, no-no!

Nous, on veut – ... d’accords.  [Chorus repeats]

[1]
Nous sommes des oiseaux de passage,
We are birds of passage;

Jamais docile ni vraiment sage. 
Never docile; nor yet truly wise.

Nous ne faisons pas allégeance
We don’t pay allegiance 

A l’aube, en toute circonstance 
To the dawn, in all circumstances:

nous venons briser le silence.
We come to breach the silence!

Et quand le soir a la télé
And when in the evening on TV

monsieur le bon roi  parlé
The “good king” has spoken ...

venu annoncer la sentence
Has come to announce the sentence, [of the court] / [just speak]

nous faisons preuve irreverence
We show irreverence,

Mais toujours avec elegance
But always with style (or elegance).

Oh non-non non-non non ...
Oh no-no no-no no-no!

[CHORUS]
Nous, on veut – ... non-non.
Nous, on veut – ... d’accords

[2]
Auto, métro, boulo, conso
Drive, ride, work, buy;

Auto attestations, qu’on signe,
Auto attestations that you sign;

Absurdités sur ordonnance.
Prescription absurdities;  [or "Nonsense on prescription"]

Et malheur a celui qui pense!
And woe betide he who thinks!

Et malheur a celui qui dance!
And woe betide he who dances!

Chaque mesure authoritaire,
Each authoritarian measure,

Chaque relent securitaire
Every whiff of security

Voit s’envoler notre confiance
Sees our confidence fly away.

Ils font preuve de tant d’insistance
They manifest such insistence

Pour confiner notre conscience
To confine our consciousness.

Oh non non-non non-non non!
Oh no-no, no-no, no-no!

[ M u s i c a l  I n t e r l u d e ]

[3]
Ne soyons pas impressionable
Let's not be suggestible

Par tous ces gens déraissonable
By all these unreasonable people

Vendeur de peur en abondance
Sellers of fear in abundance                          

Angoissant jusqu’a l’indécence!
Harrowing, to the point of indecency

Sachons les tenir à distance
Let's keep them at bay.

Et pour notre santé mentale
And, for our mental,

Social et environnementale,
Social and environmental health;

Nos sourires, notre intelligence
Our smile, our intelligence -

Ne soyons pas sans résistance
Les instruments de leur démence!
Let's not become the instruments of their madness without resistance!          

This song really caught the zeitgeist and took off in France and elsewhere: you will find loads of places in France and then other countries where this dance/song was performed (not always videoed, of course) and mirrored in other languages. e.g.

---

Do read some other articles by me. My most important are
What’s wrong with “The Greater Good”? and
Coping with Disagreement and Being Wrong.

You’ll find them more informative and helpful than you expect.
(One reader described the second as “life-changing”)!

Subscribing is free, and always will be.

---

4 2023’s Everest: Hats, Turtles and Spectres

In 1953, when Hilary and Tenzing climbed Everest for the first time ever, everyone felt pleased for them, and uplifted. Most people – the 97% who are not psychopaths – could enjoy the fact that we – humankind – made a seminal achievement, even though almost everybody hadn’t made any contribution to that success themselves.

I heard about 2023's '"Everest" only recently.  It happened in May, and it’s quite possible you haven’t heard about it yet: surprising for a seminal achievement, eh?  Extra piquancy is added to the 2023 breakthrough because this one – like so many leaps forward – was largely accomplished by an enthusiastic amateur (with later help from some professionals). How appropriate that this historic victory occurred while some fools are trying to introduce a technocracy – rule by so-called “experts”.

The achievement wasn't in the field of mountaineering, but mathematics – but HANG ON, BEAR WITH ME! The great thing about this achievement is that it can be seen and appreciated by even the least mathematically-minded!

(And it is perfectly possible for non-mathematicians to thrill to mathematical achievement even when it’s not so easy to understand as this one. Here's Simon Singh:

“In 1996, working with John Lynch, I made a documentary about Fermat’s Last Theorem for the BBC series Horizon. It was 50 minutes of mathematicians talking about mathematics, which is not the obvious recipe for a TV blockbuster, but the result was a programme that captured the public imagination and which received critical acclaim.
…
The documentary was about mathematics and mathematicians, but it was also about childhood dreams, ambition, obsession, passion, failure and triumph. Not surprisingly, there was a time when one of the Hollywood studios put in a serious bid to make a feature film...

The emotion of the documentary is clear from the first minute. The opening sequence shows Professor Andrew Wiles recalling the moment when he realised that he had solved Fermat’s Last Theorem and achieved his childhood dream. The memory is so moving that he begins to stumble over his words. He then pauses, takes a breath, tries to continue, but eventually he is overcome with emotion and turns away from the camera. There are other moments in the programme that are equally emotional.)"

Now, unlike the proof of Fermat's Last Theorem, this achievement is easy to understand; it does require a little explanation though.

Suppose you are tiling a wall, or covering some ground with paving slabs. There are certain shapes that are convenient for covering the surface without leaving gaps or overlaps. The most obvious are Regular triangles, rectangles, and hexagons ("Regular" meaning sides and angles all the same)

Besides those three, no other Regular shapes ones will fit together. 

But Irregular ones (i.e. with sides that are not all the same length) can obviously work too:

You can also use combinations of different shapes. Here’s one pattern consisting of regular triangles, rectangles and hexagons:

… and one with stars and rhombuses

… and so on.

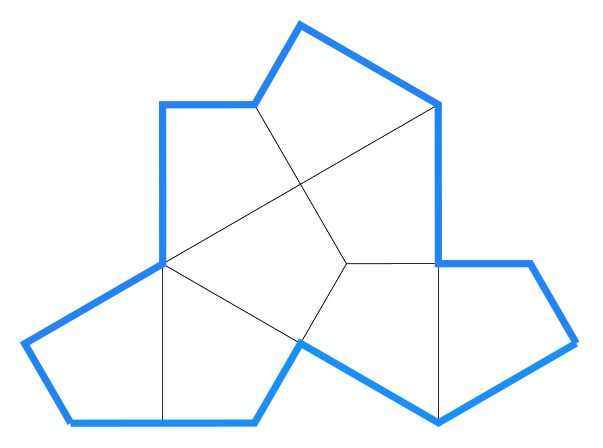
These triangles have been modified to have a bump on one side, and a notch on another.

It’s easy to see that all these patterns could extend indefinitely into the distance, as they are PERIODIC, that is to say you can take part of the pattern and move it along a bit until it is sitting on an identical pattern; and you are quite clear that those repetitions could continue indefinitely.

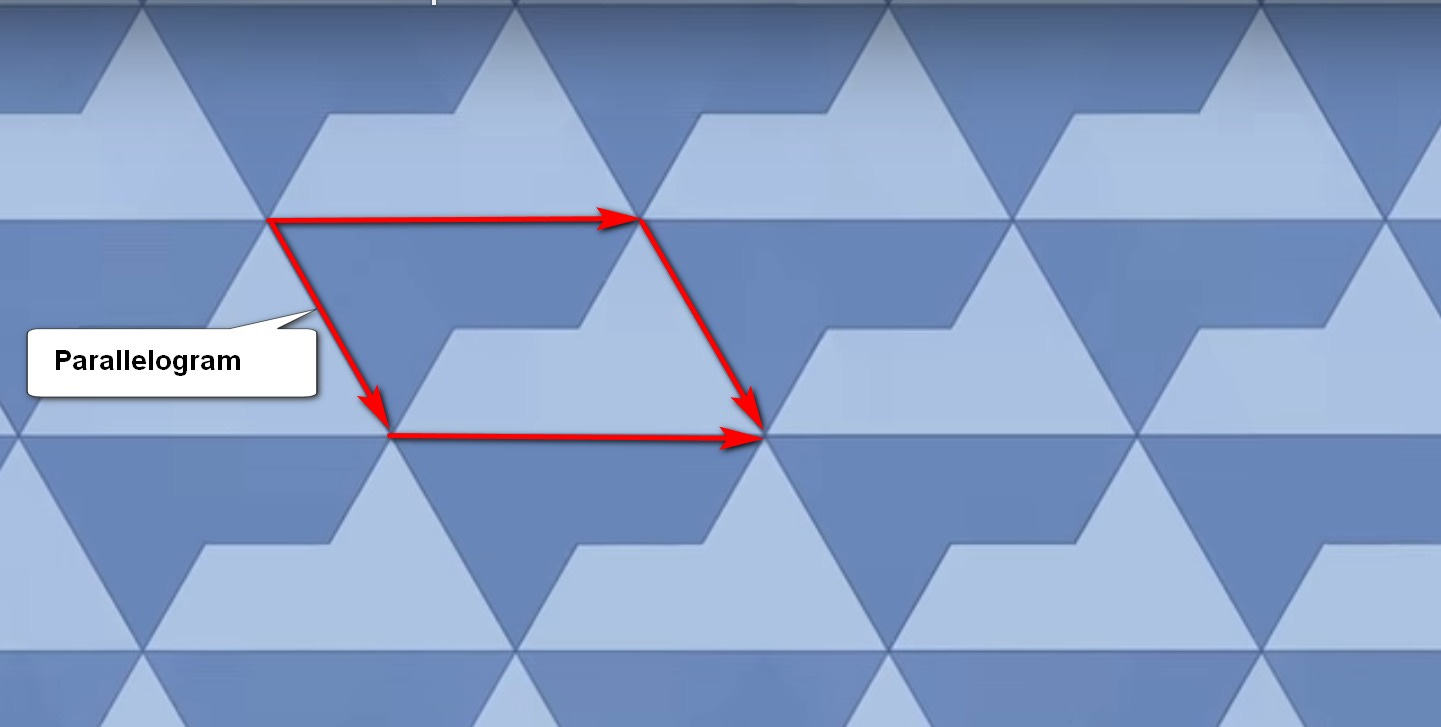
These parallelograms will obviously tile a plane periodically, like this:

… and you can see that each parallelogram has here been divided in two, to make two identical “sphinx” shapes. Take these apart and fit them together differently, and you find a non-periodic pattern – one where the pattern never repeats!  

You can find small areas that are the same, but at the edge of those areas there will be differences.  The longer you look, the larger areas that are identical you can find; but it is impossible for there not to be differences ultimately. So this shape can tile a plane periodically (paired into parallelograms) OR non-periodically.

Are there some shapes that will ONLY tile the plane non-periodically (called "aperiodically")? In the 1960’s a mathematician named Wang conjectured that that was impossible: that if a shape will tile the plane non-periodically (chaotically), it must also do so periodically. However he was soon proved wrong.

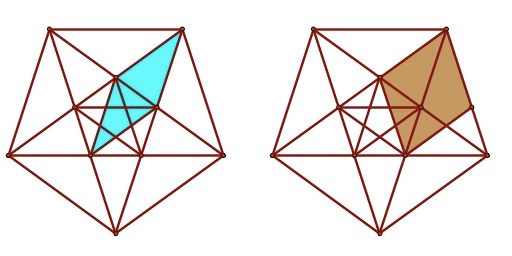
Skipping a bit of history, in the 1950’s the mathematician Roger Penrose came up with three groups of simple tiles that will cover a plane indefinitely, but aperiodically (the pattern changes continually, and cannot repeat). He chose patterns based – surprisingly – on 5-fold symmetry, which as you saw above, is not a promising start.

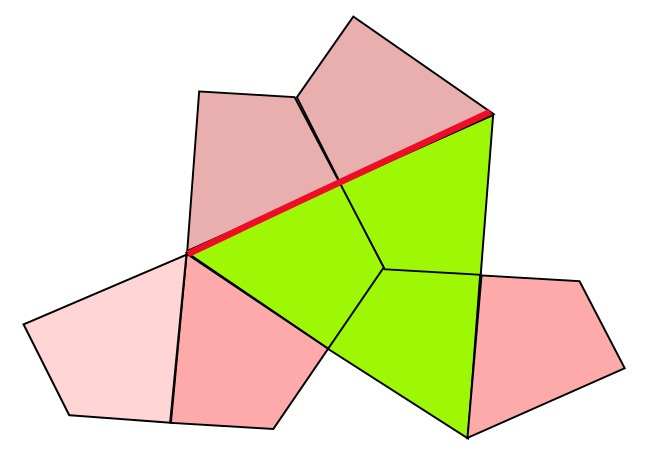
1 This tesselation (tiling pattern) of Penrose’s uses 4 shapes: a pentagon, a pentagram star, a rhombus, and a “jester’s cap” piece of a pentagram.

2 He then managed to simplify it to just 2 shapes! Two rhombuses, based on a pentagon -

3 ... and these 2 shapes, called a “kite” and “dart” (also based on a pentagon).

If these two shapes are put together as in the picture above, they form a rhombus, and will therefore tile Periodically; Restrictions are therefore put on to stop this, such as these lines (see bottom of next picture) which must match.

People were enthusiastic about this pair; and in a celebratory mood, a toilet paper company put crimps - in the shape of tessellated kites and darts - in one of their brands of roll.  Now I've been rather a fan of Penrose, partly because of these very accessible ideas, and partly because he holds heterodox views about the nature of matter.  But he sued the company, on copyright grounds; and they had to stop making paper with this pattern.  This episode tends to diminish his heroic stature in my eyes: apart from appearing curmudgeonly, it also raises the philosophical question of when you expand what is known about mathematics, is that an invention or a discovery?  An invention would be patentable; presumably a discovery would not.  I would have thought that mathematicians would prefer the more purist view that it is a discovery of something that has always been true, rather than an invention of something new.  You can still get the kudos as the discoverer.  More here.

Is it possible to improve on a pair of shapes, and find a single shape that will aperiodically tessellate (tile a plane infinitely, and only in a "chaotic pattern")?  

During the 50 year search it was nicknamed the "einstein" tile: German for "one stone": geddit?!

In March this year - 2023 - a gentleman with the suitably “Everyman” name of Dave Smith managed to find one, for the first time!

Here's a video of someone explaining the situation and its effect on her.

Now, I'm not suggesting that this was the route that Dave Smith took, but this might be a reasonable way to arrive at the destination.  We're looking for a shape that is going to fit together well, so the angles that make it up might well be those you find in regular triangles, rectangles and hexagons.

If we start with a triangular grid (in pink) then join the centre of each triangle together,

we find that we have made a hexagon, in fact a grid of hexagons.

(We could arrive at the same place by drawing a grid of hexagons, and joining the centre of each hexagon together, making an interlocking grid of triangles).

Now look for a shape that uses a (regular) "triangle" angle, a "rectangle" angle, and a "hexagon" angle - i.e. 60, 90 and 120 degrees. 

That kite shape looks promising.  It has all those angles, and it's rather like the "kite" shape that Penrose used together with the dart, except the angles are from a 6-sided figure not a 5-sided one.

If we put some kites together, probably in a way that is asymmetrical, perhaps we can come up with a shape that tessellates (tiles) aperiodically (in a chaotic pattern)?

Eventually, Dave came up with this shape, consisting of 8 kites, made some models of it, and started fitting them together.  He called it the “Hat” (although most people prefer to see it the other way up as a shirt)!

They seemed to go on fitting together, and they were not obviously periodic.

Dave called in some professional math's buddies, and they checked. Yup, they could prove that it was aperiodic in a couple of quite simple ways.  

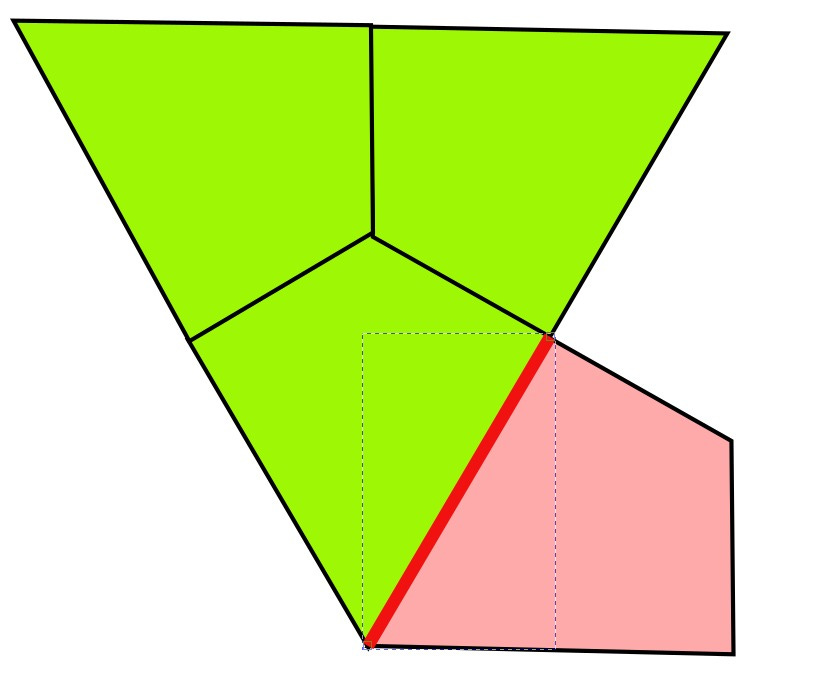
If you want to remember the shape, try this.  Put 3 kites put together to make an equilateral triangle, then reflect one of the kites to add another.

Go to the next side and reflect twice

Go to the last side and reflect both. The resulting shape is the "Hat"

Yes - it is a single slab that will pave a plane, in an aperiodic way: it cannot tile it periodically!

However, when you use the "Hat" shaped slabs some of them need to be turned over - the mirror image shape. Compare the grey and white shapes in the diagram above.

So if you are making paving slabs, then yes, it is a single shaped slab that will tile a plane.  But if you are making tiles, with one side glazed, you need to make some with the other side glazed. It is not a perfect monotile in that respect.

While the mathematicians were working on the proof,

Dave came up with a second shape!!

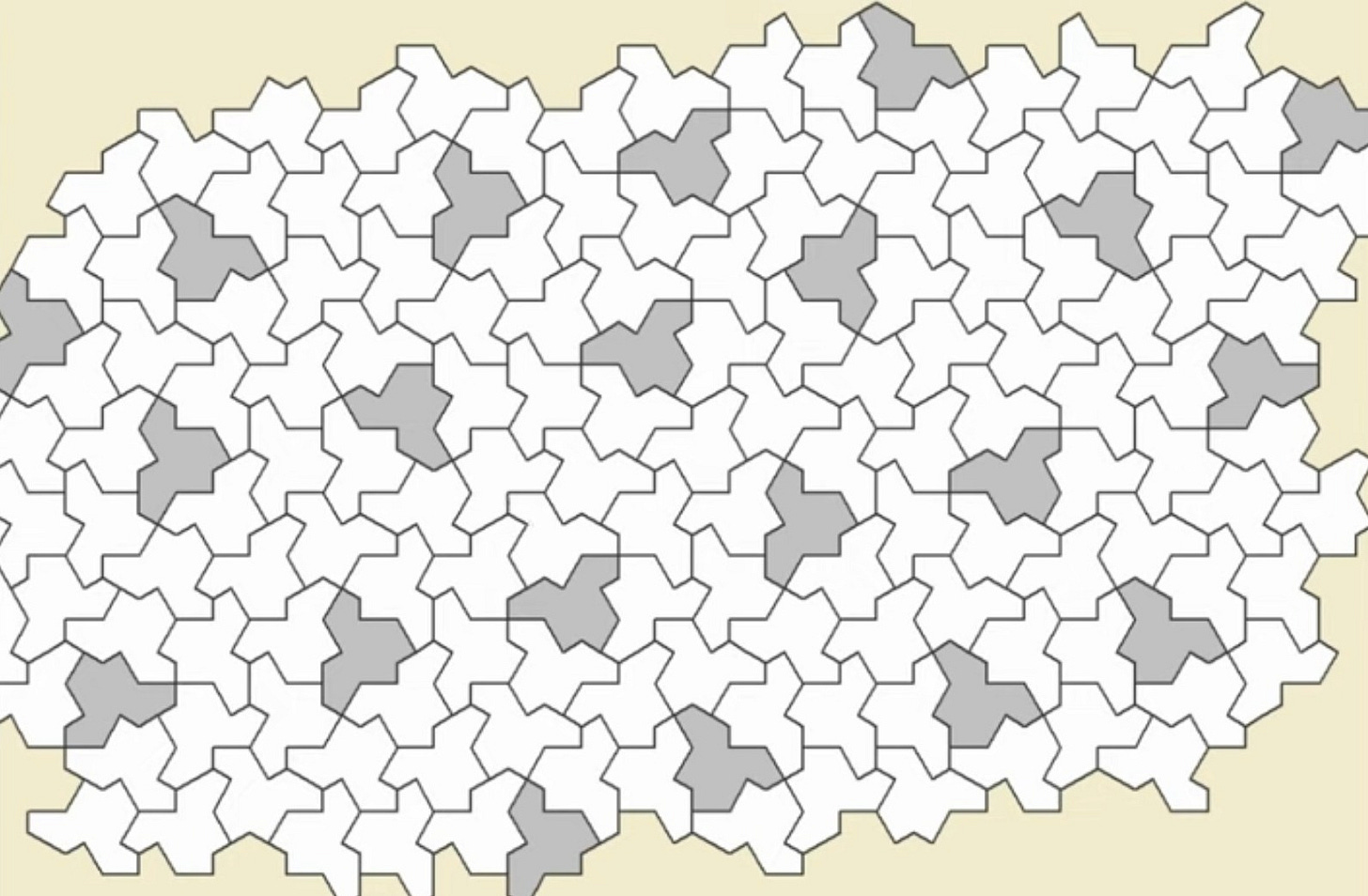
made of 10 kites, that will behave the same - tile a plane aperiodically.  People had been looking for it for 50 years - or forever, depending on how you look at it - and within a couple of weeks Dave had found two!

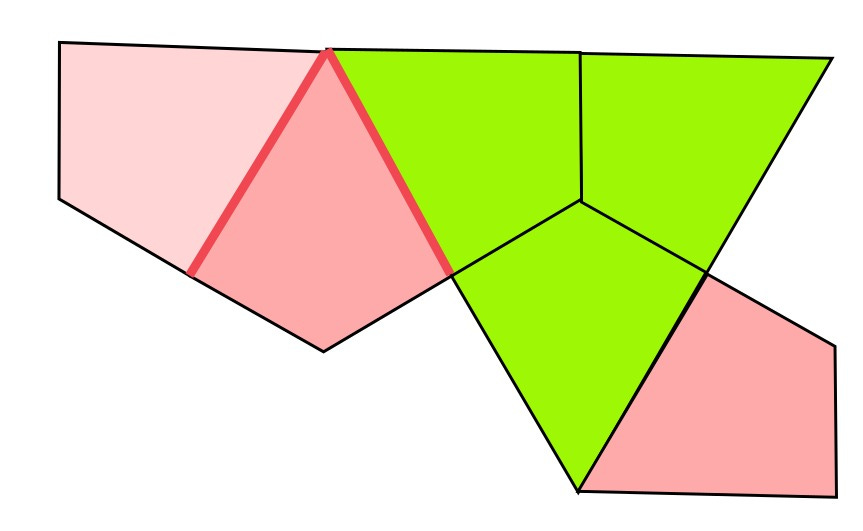
One of the mathematicians (Joseph Myers) noticed a relationship between the two shapes. In the next diagram the turtle is up-side-down. (Of course that would not be necessary if they had just called the Hat a shirt like everyone else)!

If you start, say at the bottom left corner of both shapes, and move to the right past two kites, you get to a vertex where you turn 60 degrees left up the page, then turn right 90 degrees, then left 60 degrees ... and so on all the way round.  The kites have two different lengths: the only difference between the two shapes is that the long and short sides are swapped around. Compare a red section or blue section of the two shapes.

So it turns out that that first thought - using the angles from a regular triangle, rectangle and hexagon is the important part.  The lengths are not important, as long as you use the same short and long size throughout one tile. Rather than seeing the shape as a bunch of a particular shapes put together, perhaps it is better to think of it as collection of 7 lines with a 60 degree bend in, which all get connected at 90 degrees (or a multiple thereof). For confirmation of this, look at the central shape in the “spectrum” below. It shows the case half-way between the Hat and the Turtle, where both sets of lines are the same length. Look what has happened to the “kites” from the Hat - all distorted. Then consider that the Turtle had two extra kites in there!

The kite shapes were only useful to get the angles right.

So there is a continuum along which you can change the proportions of the two lengths, all the way from the "blue" sides reduced to zero, on the left, to the "red" sides being reduced to zero on the right.  Those two extremes are reduced in complexity, and can tile the plane periodically (but also non-periodically, I believe).  None of the shapes in between can tile the plane periodically, except the very central one, where the "red" lengths and the "blue" lengths are the same size.  They quickly spotted that the central "Regular" (all lengths the same) shape can tile periodically, like this …

The four of them published a paper in March 2023 - "An Aperiodic Monotile". 

Then Dave (again) came up with a third seminal observation!!

And this is the best. What do you notice about that in that blue Periodic tiling above?  The tiles alternate in which way up the tile is - its "handedness" or chirality.  What happens if you only allow one handedness, like making tiles glazed on only one side so they all look identical?  Will they still fit together?  

Not only will they fit together, in a non-periodic way, but they cannot tile in a periodic way.  This is a true Aperiodic tile - the monotile.  (Because you have to stipulate that the shapes are all the same way up (chirality) mathematicians call it "weakly aperiodic").

However, if you modify the sides in any non-symmetrical way, you can make a tile that will not fit if you turn it over.  A simple (asymetric) curve will do, as long as you do the same to all the sides; or if you want to use only straight lines, you can put a little notch and bump on each length.  Then you have an un-arguable "monotile".

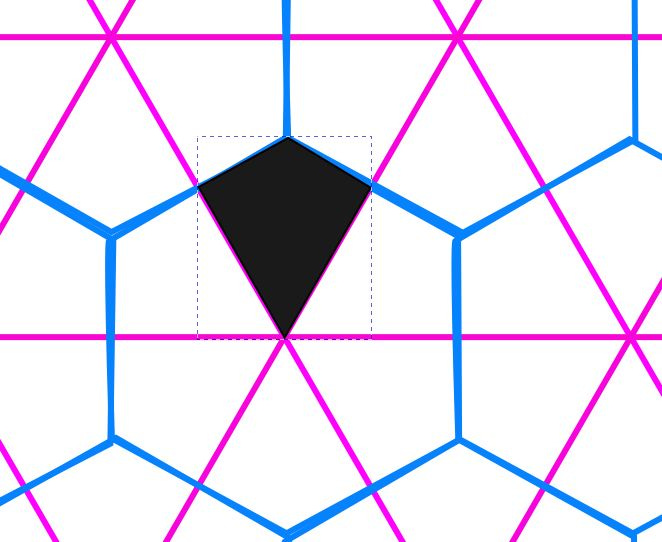
This "central" shape on the spectrum - all sides the same length is called the "spectre", and if you curve the sides it does look quite spectral.

So if you want to pave part of your garden, but don’t want regular, straight rows, one of the above three shapes would guarantee uniform paving with a certain measure of chaos.

Using a simple drawing programme like Inkscape gives you the ability to tweak those curves in all sorts of creative ways …

giving all sorts of artistic possibilities.

… and necessitating a second paper, in May this year - 2023: The Year of the Spectre!

Not only did the amateur, Dave Smith, come up with the first two aperiodic monotiles, he beat the other three mathematicians he was “working” with, who had the same information he did, to the final breakthrough - the best “einstein”.

I’m sure one could draw several “morals” from this true story. For me, it’s simply

“Play is important”.

Play is an excellent way to learn and a good de-stressor at any time, but particularly important at a Time of Lies, in an era of Shitfuckery.

---

Helpful Videos

Good quick explanation from Jade Tan-Holmes

Engaging video on tessellation from before this breakthrough, by Veritasium

Transformation Hat - Turtle animation by Craig Kaplan (one of the mathematicians).

Interview with Craig on the events.

Instructions for drawing such shapes with a free drawing programme, Inkscape.

1. Latin for “gold from in among the dung”. I first came across this ancient saying from an autobiographical story by Primo Levi, in “The Periodic Table”. Curiously, I refer to another book of his - “Moments of Reprieve” - in this article; which is about time he spent in Auschwitz, as an Italian Jew, during WW2. Interesting that such material should come to mind now, when it may not be long before some of count ourselves lucky to be in work-camps or ghettos, aka “15 minute cities”.

2. Topical at the time in the UK was general amusement when, after money had been spent making the national railways more proof against snow, there were extensive stoppages after a little snow. When queried about how this could be, the reply was “it was the wrong sort of snow” (which had “blocked their lines”)!

3. https://www.linguee.com/french-english/translation/grille+d%27accords.html